Nous allons nous intéresser, dans cette partie, à l’objet même du modèle et à sa création.

1) Traduction mathématique d’une Situation épidémique

Il existe deux types de modèles adaptés à l’étude des maladies infectieuses : Les modèles déterministes et les modèles stochastique. Nous allons voir leurs principes et leurs différentes utilisations.

a) Modèles déterministes

Nous allons nous intéresser dans un premier temps aux modèles déterministes qui proposent une vision générale de la population et divisent celle-ci en plusieurs catégories de personnes ayant, à un instant t, une certaine “position“ par rapport à l’infection. Ils permettent ainsi de voir l’évolution d’une épidémie en traduisant les phénomènes ayant lieu en moyenne, à l’échelle d’une grande population.

Le nombre et les caractéristiques de ces différents « groupes », sont déterminés par les particularités de l’agent pathogène* et par l’histoire naturelle de la maladie, d’où la nécessité de l’observation et de solides connaissances biologiques sur le sujet (voir partie Observations).

Ensuite, le modéliste doit alterner entre observation et intuition, tout en respectant bien sûr des méthodes, pour au final créer une suite d’équations représentant aussi fidèlement que nécessaire (pour répondre au problème posé) la transmission de la maladie.

De façon intuitive et logique, on distingue lors d’une épidémie au minimum deux types de personnes :

Celles n’ayant pas la maladie qui ne peuvent donc pas la transmettre.

Celles qui ont la maladie et qui peuvent ainsi la transmettre.

Il est cependant souvent utile, pour être plus précis, de faire appel à d’autres catégories d’individus. 

Il existe un grand nombre de modèles déterministes portant pour nom les premières lettres de chacun des compartiments qu’ils prennent en charge. Par exemple le modèle SIR inclut des Susceptibles, des Infectieux et des immuns (en anglais Recovered) ; Le modèle SEIR y ajoute entre les phases de susceptibilité et d’infection, une étape d’exposition à la maladie (E pour Exposed).

Nous allons, pour expliquer la modélisation, prendre l’exemple du modèle SIR, simple mais intéressant. 

On a ainsi, à un instant précis de l’épidémie, trois états possibles par rapport à la maladie :

Susceptible

Infecté

Immun : Cette catégorie regroupe toutes les personnes ne pouvant pas ou plus être infectées : d’une manière générale, elles ont soit déjà contracté la maladie (suffisamment longtemps auparavant pour ne plus pouvoir la transmettre ni en présenter les symptômes), soit ont été vaccinées (bien que le facteur d’immunité naturel soit existant), soit sont mortes.

On peut représenter ces catégories par des boites:

Au niveau chronologique, ce modèle sera utilisé pour les infections dans lesquels un individu, s’il “attrape“ la maladie, sera infecté, après avoir été susceptible (par exemple la grippe). Ensuite, la maladie n’étant pas une maladie chronique*, l’individu vas guérir et sera immunisé contre le virus. Nous prenons donc un cas dans lequel l’individu ne pourra être infecté qu’une seule fois (au moins durant la période étudiée).

On a alors :

A ce stade là, on ne prend aucunement en compte le fait que toutes les personnes de la population ne sont pas obligatoirement infectées lors d’une épidémie : à l’état de “susceptible“, le “risque“ d’infection n’est pas total. Il existe donc des formules mathématiques traduisant le passage des individus d’une catégorie à l’autre. Ce sont des fonctions prenant en compte des taux de transitions*.     

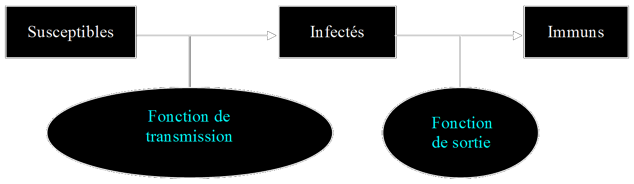
Comme le montre le schéma, une fonction très importante et intéressante du modèle déterministe est la fonction de transmission*. Il en existe de nombreuses, plus ou moins précises, qui ont toutes des avantages et des inconvénients par rapport aux résultats recherchés (là encore, le choix revient au modéliste).

    Fonctions de transmission

Nous allons en étudier deux différentes, mais il faut savoir qu’il en existe un grand nombre. Commençons par la plus intuitive : 

NI = β.S.I

Avec : NI : Nombre de nouveaux infectés

   S : nombre de susceptibles

   I : Nombre d’infectés

            β : est le facteur de proportionnalité qui traduit en quelque sorte les probabilités, pour un individu sain “d’attraper“ la maladie, en fonction du nombre d’infectés et de susceptibles. On observe que c’est lui qui régit en grande partie le fonctionnement du modèle : Il doit prendre en compte des facteurs biologiques (la maladie, son histoire naturelle…), des facteurs sociologiques (contacts entre les individus de la population). . . Tous les éléments pouvant agir sur la transmission de la maladie peuvent y être inclus, à condition de ne pas fausser l’analyse ou de la rendre trop complexe.  

Tout en restant dans le  “général“, on peut décortiquer cette équation :

dI/dt=S.c.p. η

Avec :  dI/dt : Nombre de nouveaux cas infectieux par unité de temps.

            S : Nombre total de personnes dans la population.

            c : Le taux de contact (t -1)

            p : La probabilité que le contact soit avec un sujet infecté : P= I/S

(Avec  I nombre de personnes infectées dans la population)

            η : La probabilité de transmission lors d’un contact avec un sujet infecté.

De façon plus littéraire, dans l’ensemble de la population S, il existe un taux c qui traduit le nombre de contacts entre les individus de la population dans un temps donné. Tous ces contact ne se font pas obligatoirement avec une personne infectieuse, d’où le facteur p, qui permet de calculer les risques de fréquenter une personne pouvant transmettre la maladie. De plus, même en fréquentant une personne infectée, il est possible de ne pas l’être à son tour : tous les contacts ne sont pas infectants, d’où le facteur η qui va en quelque sorte traduire le risque de transmission qui existe, lors d’un contact entre un individu susceptible et un individu infecté.

    Remarque : On appelle Force d’infection l’ensemble des termes C.P.η. Cette appellation traduit de façon “logique“ ce produit : plus celui-ci est élevé, plus la maladie aura de chances de se propager. C’est elle qui donne ainsi le taux d’individus sains devenant infectés.

Les mathématiques, ainsi que la biologie sont en constante évolution, fruits de nombreuses recherches ; il existe donc plusieurs formules traduisant, de façons différentes l’évolution des nouveaux cas lors d’une épidémie. Prenons par exemple la formule de reed&frost.

Avec la formule précédemment étudiée, le nombre de nouveaux cas est égal au produit : ß.S.I.

Autrement dit, le nombre de nouveaux malades est proportionnel au nombre de contagieux et de réceptifs (le nombre de nouveaux infectés sera d’autant plus grand qu’il y aura beaucoup de contagieux et que la population sera grande). Le facteur beta dépend quand à lui de la maladie elle-même et de son histoire naturelle, certaines maladies se transmettant plus facilement que d'autres (Voir partie Observation).

Cette formule, bien que fonctionnelle, comporte cependant un grand défaut, puisqu'elle n’intègre pas le fait qu’il est impossible pour un sujet sain d’être contaminé deux fois ou plus au contact de plusieurs sujets contagieux. (Un individu infecté statistiquement plusieurs fois ne sera dans la réalité qu’une fois malade).

    Reed&frost ont alors eu l'idée de prendre le problème à l'envers : ils ont calculé les chances qu’avaient les individus sains, de ne pas contracter la maladie. Ils ont donc adopté la formule :    

1- β

Avec β : Probabilité de contact (infectieux)

Celle-ci correspond aux chances de ne pas attraper la maladie en présence d'une seule personne malade.

En présence de deux contagieux, les chances d’être contaminé sont de

1- β par individu infecté fréquenté. Cela se traduit par :

(1- β)*(1- β) = (1- β)²

En présence de trois malades on pendra (1-beta)^3 et ainsi de suite.

Vous l’aurez compris, d’une manière générale, les risques, pour une personne saine d'attraper la maladie seront donc de :

1-(1- β)^I

Avec :    I : Nombre de contagieux

Pour connaitre le nombre de nouveaux cas, il suffit alors de multiplier cette formule par le nombre de personnes saines :

NI = (1-(1- β)^I)*S

Avec :  NI : Nombre de nouveaux cas.

           (1-(1- β)^I) : probabilités d’infections

           S : Nombre de susceptibles.

Le modèle

L’ensemble de cette théorie déterministe donne lieu à un ensemble d’équations permettant de déterminer les évolutions de la population dans les trois “groupes“ (elle prend en compte dans le cas présent, la première formule étudiée):

     dS/dt =  β(S,I,R) – δS – βSI +  qR

    dI/dt =  βSI - aI – rI

dR/dT =  rI – δR – qR

 

Avec

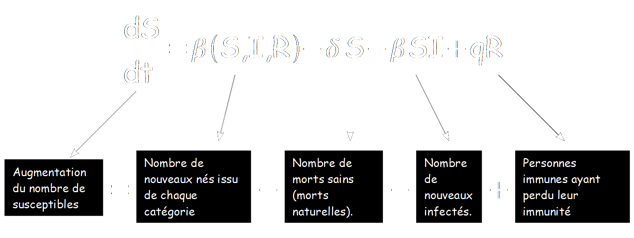
En effet, les nouveaux susceptibles sont d'abord tous les nouveaux nés, puisque l'on parle ici d'une maladie ne se transmettant pas de la mère à l'enfant (β(S,I,R)). A ceux-ci s'ajoute l'ensemble des personne immunes ayant perdu leur immunité (qR).

On doit cependant soustraire à ce groupe les morts appartenant à cette catégorie (δS) et bien évidement le nombre de nouveaux infectés.

Le principe est le même pour les deux autres membres du système :

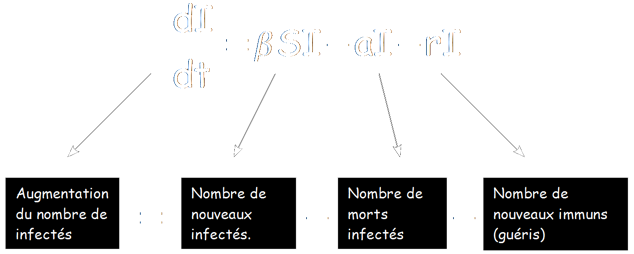
Il est juste utile de faire quelques précisions :

Le membre aI prend en compte les morts naturelles ainsi que celles dues à la maladie (avec a : taux de décès dus à la maladie et naturels)

Le facteur r est le taux de personnes guérissant (par rapport au temps), ainsi rI sera le nombre de nouveaux immuns.

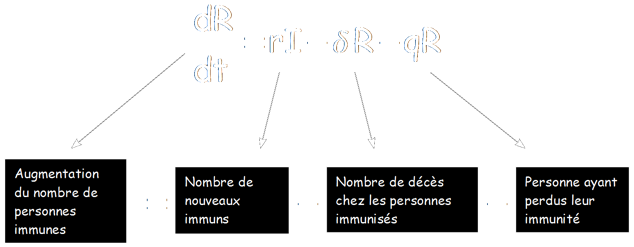
Ces formules présentent l'augmentation du nombre d'individu dans chaque catégorie : La formule dS/dt traduit par exemple une augmentation (ou diminution de nombre de susceptibles), il s'agit donc d'une fonction dérivée (fonction faisant varier la pente de la courbe épidémique) : on peut alors dire que dS/dt = S'(t), puisqu'il s'agit de la dérivée de la fonction du nombre de nouveaux cas.

La résolution du système sera donc souvent, pour les modèles déterministes une succession d'équations différentielles*. 

b) Modèles stochastiques

            Les modèles stochastiques conservent le principe de catégories d’individus par rapport à la  maladie (susceptible, infecté ou immun).
 Ils sont cependant basés sur des probabilités et utilisent toujours des nombres aléatoires. Ainsi ne donnent-ils jamais le même résultat, ce qui constitue leur principal avantage. Ces modèles laissent place à l’imprévu et peuvent prendre en compte tous les cas de figure (du plus attendu au plus surprenant). Ils sont donc adaptés à l’étude de petites populations au sein desquelles le taux de contact peut varier profondément (contrairement aux grands groupes dans lesquels une moyenne s’établit naturellement). Un sujet infecté peut aussi bien rencontrer tout les suspects du groupe que rester isolé et ne voir personne.
On peut aussi noter que les modèles stochastiques sont plus adaptés à l'étude de petits groupes de personnes parce qu’ils suppriment certains effets aléatoires* apparaissant dans les modèles déterministes pour ce type de population.

            Au niveau fonctionnel, les modèles stochastiques marchent par “tours“, entre lesquels chaque individu peut passer de susceptible à infectieux, ou d’infectieux à immun (pour un modèle SIR bien sûr). On choisit en général plusieurs hypothèses qui simplifient significativement le modèle : on choisit Δt (période entre deux instants calculés par le modèle/tours) égal à la période d'incubation de la maladie, de telle sorte que si un individu est contaminé au temps t=0, il sera contagieux à l’instant t=1 puis immun au temps t=2. Par ailleurs, on suppose qu’un individu contractant la maladie peut la transmettre  immédiatement : il n'y a pas de temps de latence. Enfin, on considère que les immuns restent immuns et ne redeviennent pas susceptibles.

Il existe plusieurs méthodes pour modéliser de façon stochastique.
L’une d’entre elle se base sur le suivi de chaque individu de la population au cours du temps.
A l'aide de la formule de reed&frost (vue précédemment), on calcule λ, le risque pour un individu susceptible d'attraper la maladie :
λ = 1 - (1- β)^nb de contagieux

La modélisation débute au temps t=0 avec un certain nombre d'infecté(s), de susceptibles et d'immun(s)
Pour chaque individu suspect de la population, un nombre aléatoire, compris entre 0 et 1, est tiré : ( pour que le modèle soit le plus juste possible il est préférable de prendre n avec autant de chiffres significatifs que λ)
- si n est plus grand que λ, l'individu a de la chance : il n'est pas infecté (ou du moins pas pour l’instant).
- si n est inferieur à λ, il devient contagieux.
On s'intéresse ensuite aux individus contagieux : Ceux- ci ne deviendrons immuns qu’une fois le temps de contagion de la maladie dépassé mais conserveront ensuite cet état (il n’y a pas de retour à la catégorie susceptible).
Tous les calculs seront régis par les mêmes règles au temps t=2 ; t=3 … Jusqu’à ce qu’il n’y ait plus d’infectés. L’épidémie sera alors terminée.
Remarque : le modèle ne donnera (presque) jamais les mêmes résultats, du fait de l’existence des nombres aléatoires dans la formule.

Au niveau formel, il est intuitif de représenter ce type de modèles par un tableau (évolution des individus en ligne en fonction du temps, en colonne).

Voici un exemple que nous avons créé :

2) Des modèles très complexes

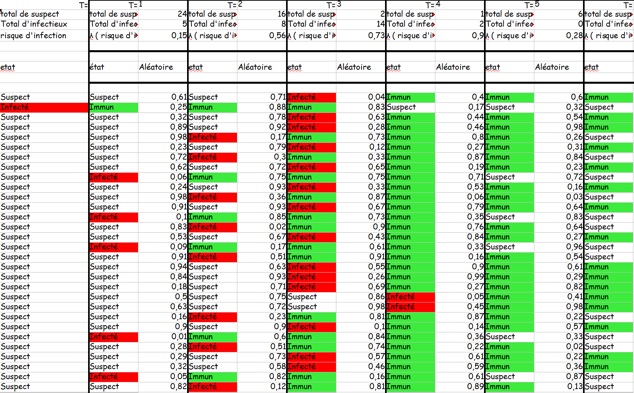
Les modèles, se basant sur les principes montrés précédemment, peuvent de par leur structure, les facteurs qu’ils prennent en compte… être bien plus précis … et beaucoup plus compliqués.

Prenons quelques exemples.

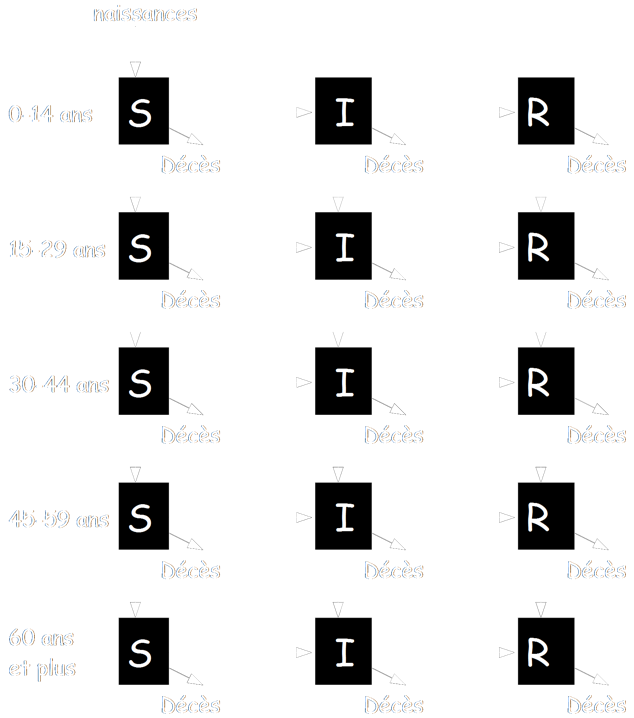
a) Les modèles structurés en âge

Certaines maladies, comme la varicelle ou l’herpes touchent différemment les individus, selon leur âge. Il n’existe donc pas le même facteur de contagiosité entre toutes les tranches de la population (les jeunes, les nouveau-nés ou les personnes âgées), et il sera nécessaire de faire un modèle regroupant plusieurs sous modèles.

Voici un exemple de structure :

b) Modèles prenant en compte les différences géographiques.

Il est indéniable qu’une maladie ne se transmet pas de la même manière sur l’ensemble du globe. Sur le plan démographique, on peut expliquer cela par le fait que les individus, selon leur lieu d’habitation entre autre, n’ont pas le même taux de contact : un individu perdu dans un village reculé du Tibet et un Américain arpentant les rues d’une grande ville, ne croiseront sûrement pas le même nombre de personnes en une journée. Ce facteur va ainsi modifier la probabilité  β, de transmission, et peut aussi être pris en compte. A cela s’ajoute les transports : les aéroports, par exemple, sont non seulement des lieux à fort risque d’infection (de part le nombre de personnes qui les fréquente), mais aussi des passages rapides, permettant à la maladie de se propager de continents en continents…

En prenant en compte tous ces facteurs, on crée des modèles présentant l’évolution d’une épidémie de façon géographique, à travers une carte par exemple :

Rouge : infectés ; Vert : sortis (immuns ou morts)

Ces images représentent l’évolution géographique d’une épidémie de grippe à travers les Etats-Unis (avec une population totalement susceptible). On remarque que les “points rouges“, zones de forte épidémie correspondent aux grandes villes Américaines.   

c) Modèles économiques

Parmi les nombreux modèles existants, certain vont aussi prendre en compte le souci budgétaire des actions de santé publique mises en place lors d’épidémies. En effet, les médicaments, vaccins, consultations …ont un coût, et celui-ci est un facteur décisionnel important. Ainsi, certains modèles ont pour but de prévoir le budget nécessaire au contrôle d’une maladie en fonction du nombre d’infectés, d’immuns…

L’industrie pharmaceutique a recours à de tels modèles pour évaluer les rapports coût/efficacité de certains traitements : le nombre d’individus chez qui celui-ci a été efficace, en fonction du prix que sa mise sur le marché a coûté.

Au final, les modèles utilisés à l’heure actuelle prennent parfois en compte l’âge, la démographie, la géographie ... Cependant, il n’est pas forcément utile de mettre en équation une quantité colossale de phénomènes. En effet, cela peut compliquer, voir fausser l’analyse du modèle, qui a pour but, rappelons le, de répondre à un problème précis.  

Voici un exemple concret, de ce à quoi peut ressembler l’ensemble des équations d’un modèle. Il s’agit d’un modèle de propagation du Papillomavirus, un virus sexuellement transmissible, qui est responsable, chez les femmes infectées, du cancer du col de l’utérus.

Une fois ces données prises en compte, certains paramètres doivent logiquement être modélisés, comme la tranche de la population ayant une vie sexuelle : cette partie de la population sera pratiquement la seule exposée (Il s’agit d’une MST).

Voici le modèle en lui-même (Ne faites pas cette tête !). Nous ne pourrons pas l’expliquer en intégralité, il est cependant intéressant de voir qu’il s’agit d’équations différentielles.  

Remarque importante : Pour l’analyse de modèles compliqués, on a parfois recours à des techniques mathématiques très complexes. On pourra aussi, pour mieux cerner la dynamique épidémique, calculer des valeurs indicatives très intéressantes, tel Ro

On appelle Ro le taux de reproduction du virus. C’est le nombre de cas secondaires générés par un infectieux, donc plus Ro est grand, plus la maladie se propagera rapidement.

Par exemple, pour la rougeole, 12 < Rorougeole < 15.

Pour arrêter et faire disparaître l'épidémie, les épidémiologistes essaient de faire en sorte que 0 < Ro < 1.

A ce moment là, la maladie ne se propagera plus et régressera. Pour cela, il faut faire jouer les facteurs modifiables.

3) Un contrôle permanent

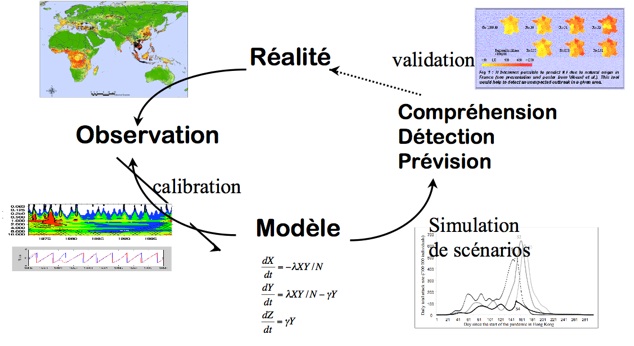
Il est très compliqué de reconnaître les facteurs traduisant le mieux un phénomène biologique. Il est donc nécessaire de valider le modèle et on a pour cela souvent recours à la comparaison. En effet, il sera primordial de comparer les résultats donnés par le modèle, aux données récoltées par l’observation. Si les deux coïncident, le modèle pourra aussi être comparé avec d’autres modèles similaires créés par d’autres équipes de recherche, avant d’être exploité. Il existe donc un réel cycle entre observation (ou récolte d’informations) et modélisation, qui entrainera une évolution du modèle à travers le temps. Celui-ci pourra en effet être réajusté et corrigé.